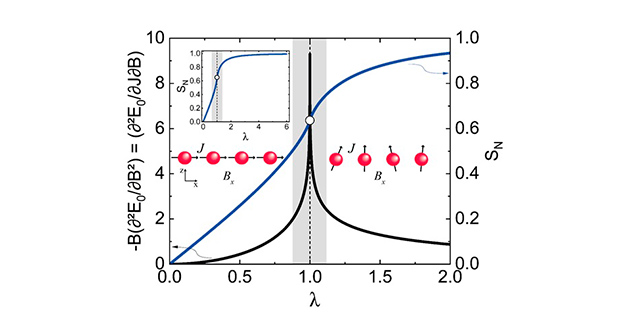
Figura publicada em Physical Review B mostra resultados indicando o aumento da entropia de von Neumann e a quebra do teorema de Hellmann-Feynman. Detalhes explicativos no artigo original (reprodução)

Publicado em 11/12/2023

José Tadeu Arantes  |  Agência FAPESP – O emaranhamento é uma propriedade da física quântica que se manifesta quando dois ou mais sistemas interagem de tal maneira que seus estados quânticos não podem ser descritos independentemente. Na terminologia da física quântica, diz-se que, nessa condição, os sistemas ficam “emaranhados”, isto é, fortemente correlacionados. Tal propriedade é de primeira importância para a realização da computação quântica. Quanto maior o emaranhamento, mais otimizado e eficiente o computador quântico.

Estudo realizado no Departamento de Física do Instituto de Geociências e Ciências Exatas da Universidade Estadual Paulista (Unesp) no campus de Rio Claro (IGCE-Unesp) propôs um novo método para quantificar o emaranhamento, bem como as condições nas quais o emaranhamento é maximizado, visando otimizar a construção de um computador quântico. O trabalho foi publicado em formato “letter” no periódico Physical Review B: “Grüneisen parameter as an entanglement compass and the breakdown of the Hellmann-Feynman theorem”.

No estudo, os pesquisadores demonstraram também que, em condições particulares, ocorre a quebra do teorema de Hellmann-Feynman da física quântica. Esse teorema descreve a dependência da energia própria do sistema em relação a um parâmetro de controle.

“Dito de forma muito resumida, nós propusemos um parâmetro de Grüneisen quântico em analogia com o parâmetro de Grüneisen da termodinâmica, amplamente utilizado na literatura para explorar pontos críticos a temperatura finita e nas vizinhanças de pontos críticos quânticos. Em nossa proposta, o parâmetro de Grüneisen quântico quantifica o emaranhamento, ou seja, a entropia de von Neumann, em relação a um parâmetro de controle, que pode ser o campo magnético ou a pressão, por exemplo”, conta Valdeci Mariano de Souza, professor do IGCE-Unesp e coordenador do estudo, à Agência FAPESP.

“Utilizando nossa proposta, demonstramos que o emaranhamento será maximizado na vizinhança de pontos críticos quânticos e que ocorre a quebra do teorema de Hellmann-Feynman no ponto crítico”, acrescenta o pesquisador. Além da contribuição à física fundamental, os resultados obtidos podem ter impacto direto na área de computação quântica.

Souza lembra que, em 1965, o químico Gordon Moore, cofundador da Intel, publicou um estudo mostrando que o número de transistores utilizados nos computadores convencionais dobraria a cada dois anos. Com os avanços tecnológicos dos últimos anos, ficou evidente que a capacidade de expansão da computação clássica estava com seus dias contados, mobilizando um grande esforço de pesquisa para a viabilização da computação quântica, liderada por empresas gigantes no ramo, como Google e IBM.

“Enquanto na computação convencional o processamento de informação utiliza a linguagem binária, construída em termos de 0 e 1, a mecânica quântica possibilita a chamada superposição de estados, o que permite que a capacidade de processamento seja expressivamente aumentada. Daí o forte interesse pelo estudo de temas como o do emaranhamento quântico”, explica Souza.

O estudo em pauta, proposto e idealizado por Souza, teve contribuições importantes de seu pós-doutorando Lucas Squillante. Participaram os pesquisadores Antonio Seridonio (Unesp – Campus de Ilha Solteira), Roberto Lagos-Monaco (Unesp – Campus de Rio Claro), Luciano Ricco (University of Iceland, Islândia) e Aniekan Magnus Ukpong (University of KwaZulu-Natal, África do Sul).

As pesquisas que levaram à produção do artigo receberam apoio da FAPESP por meio dos projetos 11/22050-4 e 18/09413-0.

O artigo Grüneisen parameter as an entanglement compass and the breakdown of the Hellmann-Feynman theorem pode ser acessado em https://journals.aps.org/prb/abstract/10.1103/PhysRevB.108.L140403.

 

Fonte: https://agencia.fapesp.br/50443